이진 탐색 트리(BS트리 : binary search tree)
- 특정 데이터의 효과적인 검색을 위해 제한점을 가지는 이진 트리
- 특정 데이터의 검색과 노드의 삽입 삭제 처리 에 효과적인 이진트리
- 트리를 구성할 때, 데이터의 탐색을 고려하여 구성하므로 탐색에 최적화된 이진트리
- 키 : 탐색 삽입 삭제 연산에서 비교의 대상이 되는 값, 이진트리 노드의 데이터를 대표하는 값, 혹은 노드를 특정할 수 있는 값
- root 기준 왼쪽 서브트리에 모든 노드의 키 값은 루트 보다 작다
- root 기준 오른쪽 서브트리에 모든 노드의 키 값은 루트 보다 크다
→ 중위순회를 통해 같은 순서 데이터(A-B-C-D) 를 만들어 낼 수 있다.
BS트리순회
- BS트리를 위한 노드 정의
typedef struct BSTnode{
struct BSTnode* left; // 왼쪽 자식을 위한 포인터
char key; // 키 값을 위한 문자 배열
char content[10]; // 데이터 필드
struct BSTnode* rigth; // 오른쪽 자식을 위한 포인터
} BSTnode;
- BS트리의 중위 순회 : 정렬된 순서로 데이터를 출력 할 수 있음
void inorderBST(BSTnode* root) {
if(root != NULL) {
inorderBST(root -> left);
printf("%c", root -> key);
inorderBST(root -> rigth);
}
}
BS트리의 노드 탐색
- 트리가 비어 있다면 탐색 실패 아니면 찾으려는 k와 현재 루트 노드의 키 값을 비교.
- k = 현재 key 이면 탐색 성공, 이때 찾은 정점은 vi 이다.
- k < ki 이면 vi의 왼쪽 서브트리를 탐색 (vi → left 로 바꾸고 처음으로 돌아감)
- k > ki 이면 vi 오른쪽 서브트리를 탐색 (vi → right로 바꾸고 처음으로 돌아감)
BS트리의 노드 삽입 연산
- k = ki 면 멈춘다
- k < ki 이면 vi 의 왼쪽 서브트리에 삽입해야 하므로, vi = vi → left 로 하고 4번으로 감
- k > ki 이면 vi 의 오른쪽 서브트리에 삽입해야 하므로 vi = vi → right 로 바꾸고 4번으로 감
- 트리가 비어 있으면 키가 k를 가지는 노드를 삽입한다. 그렇지 않으면 다시 k와 현재 루트 노드의 키 ki 를 비교하며 탐색 반복
BS트리의 노드 삭제
- 자식을 하나만 갖는 노드를 삭제하는 경우
→ [삭제한 노드를 가리키던 포인터] 가 [그 노드의 null이 아닌 서브트리의 루트] 를 가리키게 할당
- 두개의 자식 노드를 갖는 노드를 삭제 할 경우
→ 항상 특정 방향의 자식 노드를 올리는 방향으로 구현 (항상 오른쪽, 혹은 왼쪽 자식 노드를 삭제 위치로 올린다.)
Splay,AVL,BB 트리
이진 탐색 트리의 특징
- 트리의 구조와 특정 노드에 접근할 확률은 BS트리의 성능에 영향을 줌
- 트리의 성능이 구조에 영향을 받음 어떤 노드의 탐색 삽입 삭제를 위한 접근 정보를 예측할 수 없는 상황에서 최적의 BS트리 구조를 결정하기 어려움
경험으로 좋은 성능의 BS트리를 구축하는 방법
- 자주 탐색하는 키를 가진 노드를 트리의 루트에 가깝게 놓는다.
- 트리가 균형(BALANCE)이 되도록 유지 → 각 노드에 대해 왼쪽 오른쪽 서브트리가 가능하다면 같은 수의 노드를 갖게 한다.
Splay 트리
- 자주 탐색하는 키를 가진 노드를 루트에 가깝게 위치하도록 구성한 BS트리
- Splay 연산 : 최근에 접근한 노드 x를 (곧 사용할 것으로 예상하여) 루트에 위치 시켜 트리를 재구성하는 연산
- Splay 트리 : 가장 최근에 사용한 노드 x가 트리의 루트에 올 때 까지 Splay 연산을 반복하여 적용하여 생성된 이진 트리
Splay 트리의 연산
- 노드 x : 최근에 접근한 노드
- 노드 p : x의 부모 노드
- 노드 g : x의 조부모 노드
- Zig : p가 트리의 루트면, p와 x의 간선 연결을 회전 시킨다.
- Zig-Zig : p가 루트가 아니고 x와 p가 동일하게 왼쪽 자식들 또는 오른쪽 자식들이면 p와 조부모 g와의 간선 연결을 회전 시키고, 그 다음에 x와 p의 간선 연결을 회전 시킨다.
- Zig-Zag : p가 루트가 아니고, x가 왼쪽 자식, p가 (두 방향은 바뀌어도 됨) 이면 x와 p의 간선 연결을 회전 시키고 그 다음에 x와 x의 새로운 부모 g와의 간선 연결을 회전 시킨다.
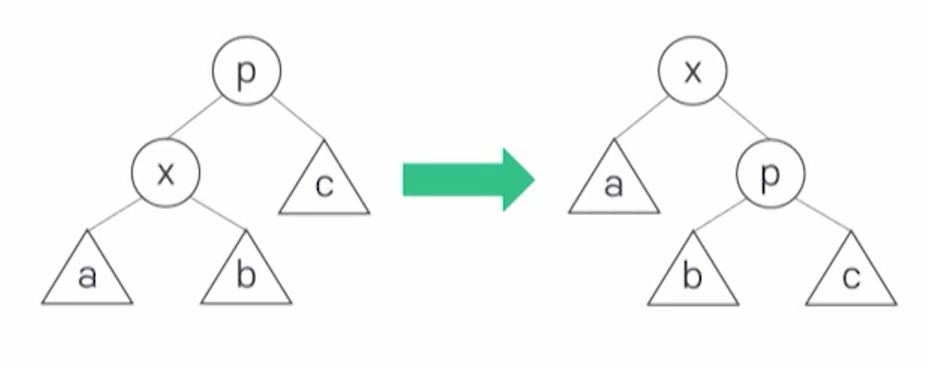
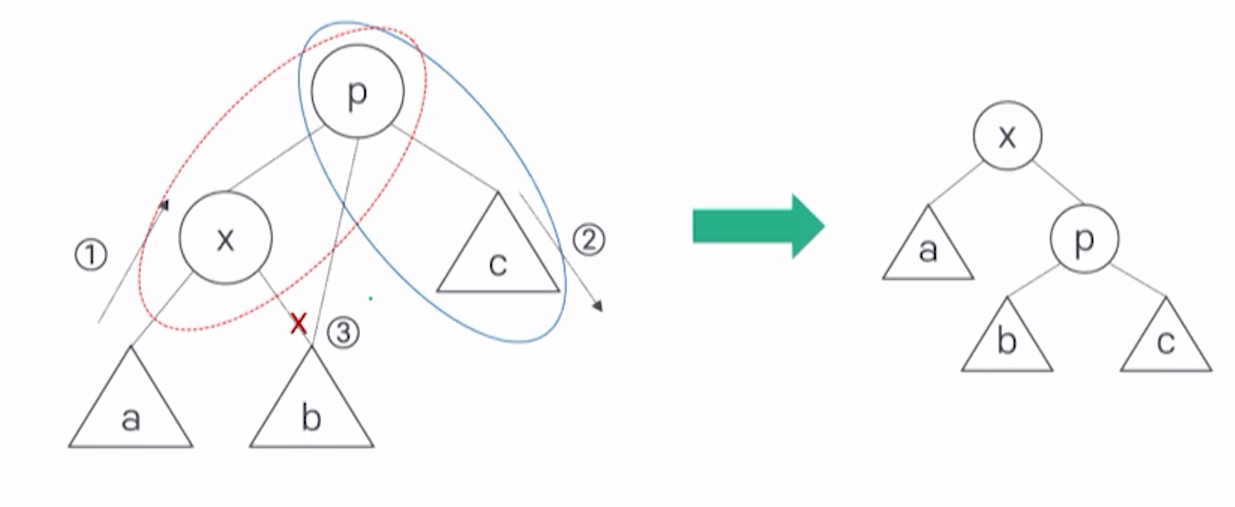
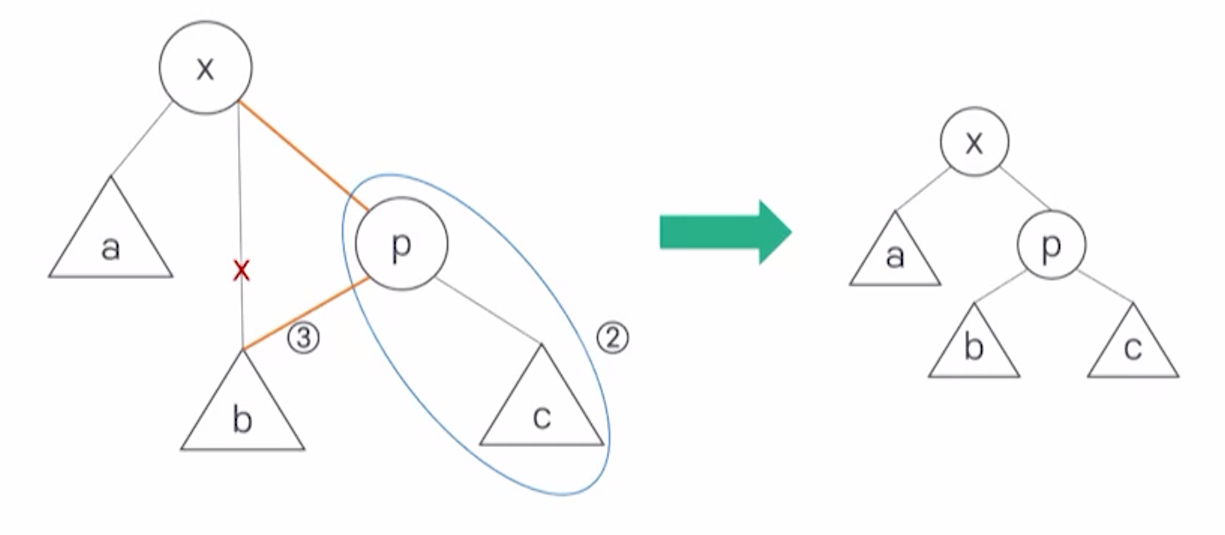
Zig
p가 트리의 루트면, p와 x의 간선 연결을 회전 시킨다.
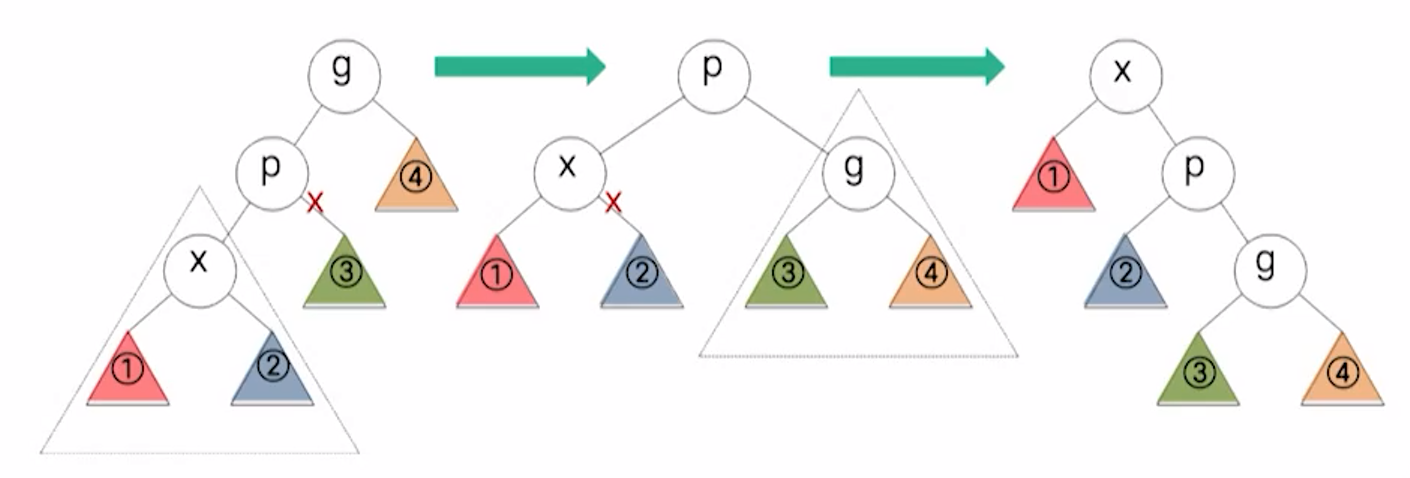
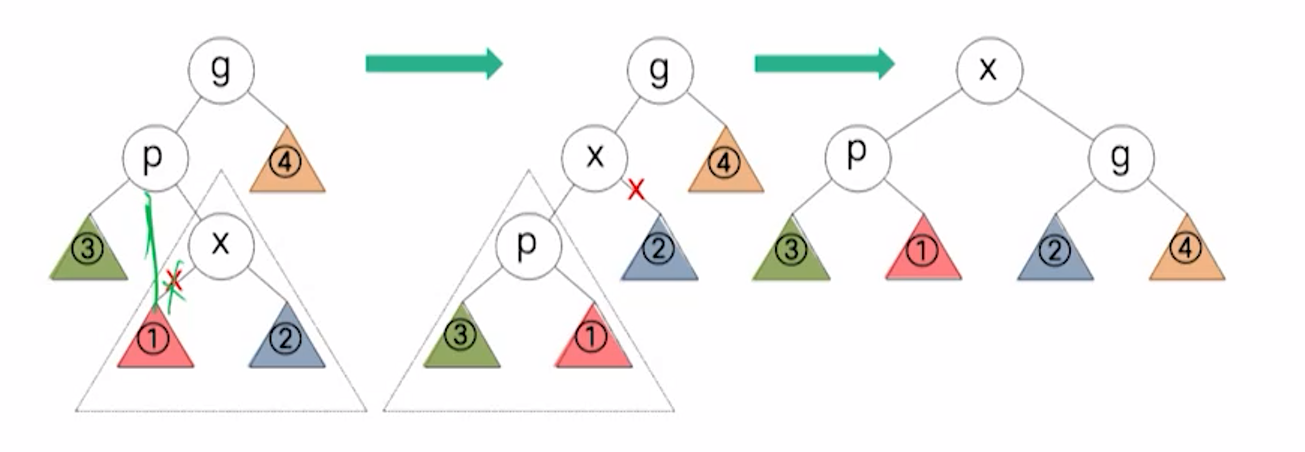
Zig-Zig
p가 루트가 아니고 x와 p가 동일하게 왼쪽 자식들 또는 오른쪽 자식들이면 p와 조부모 g와의 간선 연결을 회전 시키고, 그 다음에 x와 p의 간선 연결을 회전 시킨다.
Zig-Zag
p가 루트가 아니고, x가 왼쪽 자식, p가 (두 방향은 바뀌어도 됨) 이면 x와 p의 간선 연결을 회전 시키고 그 다음에 x와 x의 새로운 부모 g와의 간선 연결을 회전 시킨다.
변형BS트리 - AVL(Adelson-Velskii&Landis) 트리
- 노드의 삽입과 삭제가 일어날 때, 노드의 키 값과 서브트리 키 값 사이의 관계를 유지하면서 균형을 유지시키는 것이 쉽지 않음
AVL 트리의 개념
- 제한 조건을 완화하여 트리가 (완전한) 균형이 아닌 것을 허용함
- 무너진 균형의 정도는 작아야 하고, 평균 탐색 길이도 완전 균형 트리의 탐색 길이와 크게 차이가 나지 않아야 함
- 거의 완전한 균형 트리의 한 형태로 높이가 균형 잡힌 높이 균형 트리 (height balanced trre)
- 직접 탐색 성능이 매우 높음
AVL의 조건
- 노드 vi의 왼쪽 서브트리 높이와 오른쪽 서브트리 높이가 최대 1만큼 차이가 남
- 높이가 대략 균형잡힌 트리
BB트리의 정의
- BB(bound-balanced) 트리 : 거의 완전히 (대략) 균형 잡힌 트리의 다른 종류로 무게가 균형 잡힌 트리
- 각 노드의 양쪽 서브트리 무게가 균형을 유지하는 트리
균형트리
- AVL 또는 BB트리에 대하여 각각 무게 또는 크기(높이) 제한 조건을 만족 시키는데 드는 비용은 트리를 완전히 균형 잡히게 유지하는 비용이나 노력보다 훨씬 작음
- 삽입이나 삭제 후에 트리를 완전히 균형 잡히게 유지하기 위해서는 o(n) 의 노드를 옮겨야 하는 반면 AVL 또는 BB트리는 o(log2 n) 개의 노드를 옮기면 되는것으로 알려
728x90
'KNOU > 요약정리' 카테고리의 다른 글
| [자료구조] 멀티웨이 탐색트리(2) (0) | 2023.12.02 |
|---|---|
| [자료구조] 멀티웨이 탐색 트리(1) (0) | 2023.12.02 |
| [자료구조] 선택트리 , 숲 , 이진트리 개수 (0) | 2023.11.29 |
| [자료구조] 힙 (0) | 2023.11.29 |
| [자료구조] 스레드 트리 (0) | 2023.11.29 |


댓글